Ordnung im Chaos

Jeder weiß, dass beim Addieren und Subtrahieren von ganzen Zahlen wieder nur ganze Zahlen rauskommen. Alles ist symmetrisch und logisch. Für die Wurzel aus 2 hat dagegen schon Euklid in einem Beweis durch Widerspruch erklärt, dass kein noch so komplizierter Bruch die Zahl exakt darstellen kann. Wie wir gleich noch sehen werden, ist die Zahl sogar maximal chaotisch, da weder Symmetrien noch sonstige Muster in der Zahl existieren.

2. Beweis, dass die n-te Wurzel aus einer nicht x^n-Zahl irrational ist

Aus einer Zahl x, die in n gleiche Faktoren zerlegt werden kann, kann auf jeden Fall eine n-te Wurzel gezogen werden. Das ist die Definition einer n-ten Wurzel root[n]( x^n ) = x.
Jede Zahl ist in Primfaktoren zerlegbar. Aus allen Faktoren kann separat die Wurzel gezogen werden.
Angenommen wir haben eine x^n-Zahl (nach Punkt 1). Dann können wir die Zahl in Primfaktoren aufspalten. Alle Primfaktoren existieren n mal.
Beispiel: x^n = ( a*b )^n = a^n * b^n
Ähnliches kann auch für Brüche (oder Dezimalzahlen) durchgeführt werden.
Beispiel: x^n = a^n / b^n = ( a/b )^n
Eine beliebige (a/b)^n-Zahl führt durch die Wurzeloperation zu einem Nenner, der jeden prinzipiell möglichen Bruch a/b annehmen kann.
Trotzdem gibt es keine Lösung für die Wurzel von Primzahlen, da diese ja scheinbar keine x^n-Zahlen darstellen und auch nicht weiter aufgespaltet werden können.
Die Wurzel aus einer nicht eine x^n-Zahl ist somit immer irrational.
Man kann eine Zahl durch einen, beliebigen Bruch erweitern. Enthält der Bruch eine x^n-Zahl, dann kann daraus separat die Wurzel gezogen werden. Das Problem der Wurzel aus einer Primzahl bleibt aber auch bei beliebig häufigen Wiederholungen immer erhalten. Da der Bruch beliebig kompliziert sein kann, muss auch der Zahlenwert einer irrationalen Wurzel chaotisch sein.

3. Ziehen einer Wurzel

Wir möchten nun eine Wurzel einmal annähern. Man kann sich dabei immer auf ganze Zahlen beschränken, wenn man annimmt, dass man jede Dezimalzahl durch Verschiebung des Dezimalpunktes durch eine Multiplikation mit 10^n (im Dezimalsystem) um n Stellen nach rechts verschieben kann.

sqrt(2) = 1,4142135623730950488016887242097... (1)

14^2 / 100 = 1,96

15^2 / 100 = 2,25

141^2 / 10000 = 1,9881

142^2 / 10000 = 2,0164

In einem Zahlensystem p muss man im Notfall p-1 Berechnungen durchführen, um eine weitere Dezimalstelle zu ermitteln. Bei der Wurzel im Binärsystem muss entsprechend nur eine Zahl berechnet werden, um eine weitere Binärstelle zu ermitteln. Die neue Zahl wird dann anschießend noch auf größer oder kleiner bezüglich der gesuchten Zahl geprüft.

Beispiel für Quadratwurzel aus 2 (Binär 10)

2 : (2)

01^10 / 100 = 00,01 d₀₁ = 011

10^10 / 100 = 01,00 * d₁₀ = 101 *

11^10 / 100 = 10,01 * d₁₁ = 111 *

100^10 / 10000 = 01,0000 d₁₀₀ = 1001

101^10 / 10000 = 01,1001 * d₁₀₁ = 1011 *

110^10 / 10000 = 10,0100 * d₁₁₀ = 1101 *

1010^10 / 1000000 = 01,100100 d₁₀₁₀ = 10101

1011^10 / 1000000 = 01,111001 * d₁₀₁₁ = 10111 *

1100^10 / 1000000 = 10,010000 * d₁₁₀₀ = 11001 *

16:

10110^10 / 100000000 = 01,11100100 * d₁₀₁₁₀ = 101101 *

10111^10 / 100000000 = 10,00010001 * d₁₀₁₁₁ = 101111 *

11000^10 / 100000000 = 10,01000000 d₁₁₀₀₀ = 110001

32:

101100^10 / 10000000000 = 01,1110010000 d₁₀₁₁₀₀ = 1011001

101101^10 / 10000000000 = 01,1111101001 * d₁₀₁₁₀₁ = 1011011 *

101110^10 / 10000000000 = 10,0001000100 * d₁₀₁₁₁₀ = 1011101 *

64:

1011010^10 / 1000000000000 = 01,111110100100 * d_1011010 = 10110101 *

1011011^10 / 1000000000000 = 10,000001011001 * d_1011011 = 10110111 *

1011100^10 / 1000000000000 = 10,000100010000 d_1011100 = 10111001 *

Bei dem oben gezeigten Algorithmus (Heron-Algorithmus) hat die mittlere Zahl hat immer den Abstand (x-1) zum Vorgänger und (x+1) zum Nachfolger. Bei aufeinander folgenden Quadratzahlen x^2 und (x+1)^2 wächst der Abstand zwischen den Zahlen linear mit der Quadratzahl. Der Abstand d_x = (x+1)^2 – x^2 ist auch d_x= 2x+1 was einer Verschiebung des Dezimalpunktes um eine Stelle nach links plus 1 entspricht. Da eine Addition einfacher ist als eine Multiplikation, kann so der Algorithmus z.B. beschleunigt werden. Wir fragen uns jetzt natürlich wieso es überhaupt so viele Muster gibt. Betrachten wir diese nun einmal ganz allgemein.

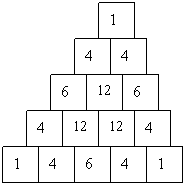
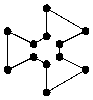
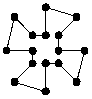
4. Anzahl der Prinzipiell möglichen Zustände

1. Wir betrachten n Punkte, die über m verschiedene Verbindungsarten miteinander verbunden werden können. Bei nur 2 Punkten ergibt sich eine Anzahl p von Lösungen, die der Anzahl an Verbindungsarten entspricht. Bei mehr Punkten lässt sich die Anzahl p über p = m^( 1+2+3+...+(n-1) ) = m^( (n-1)*n / 2 ) errechnen.

2. (2^3 = 8 mögliche Zustände) 3. (3^3 = 27 mögliche Zustände)

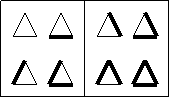
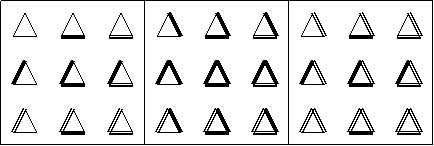
oder

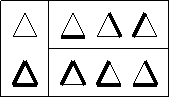
4. (2^6 = 64 mögliche Zustände)

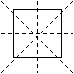5. (2^10 = 1024 mögliche Zustände)

Jedem Menschen werden die Muster und Ähnlichkeiten der Symbole schnell deutlich. Die Frage, die jetzt gestellt werden soll ist, ob der komplette Formalismus der Mathematik selber wieder so einem Muster wie oben dargestellt entspricht. Die vielen Symmetrien in „Ziehen einer Wurzel“ sprechen sicherlich dafür. Suchen wir daher nach weiteren Mustern in der Mathematik.

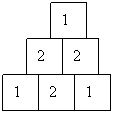
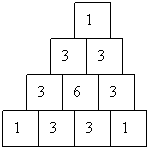
5. Ausmultiplizieren der Funktion (x+1)^n und (x-1)^n

(x-1)^0 = 1 (3)

(x-1)^1 = x - 1

(x-1)^2 = x^2 - 2*x + 1

(x-1)^3 = x^3 - 3*x^2 + 3*x - 1

(x-1)^4 = x^4 - 4*x^3 + 6*x^2 - 4*x + 1

(x-1)^5 = x^5 - 5*x^4 + 10*x^3 - 10*x^2 + 5*x - 1

(x-1)^6 = x^6 - 6*x^5 + 15*x^4 - 20*x^3 + 15*x^2 - 6*x + 1

Für (x+1)^n werden nur die negativen Vorzeichen durch positive Vorzeichen ersetzt. Es entstehen bestimmte Faktoren die wir in einer Tabelle ablegen wollen.

6. Die Binomialkoeffizienten

m=	0	1	2	3	4	5	6	7	8	9	10
n=	x^0	x^1	x^2	x^3	x^4	x^5	x^6	x^7	x^8	x^9	x^10
0	1	0	0	0	0	0	0	0	0	0	0
1	1	1	0	0	0	0	0	0	0	0	0
2	1	2	1	0	0	0	0	0	0	0	0
3	1	3	3	1	0	0	0	0	0	0	0
4	1	4	6	4	1	0	0	0	0	0	0
5	1	5	10	10	5	1	0	0	0	0	0
6	1	6	15	20	15	6	1	0	0	0	0
7	1	7	21	35	35	21	7	1	0	0	0
8	1	8	28	56	70	56	28	8	1	0	0
9	1	9	36	84	126	126	84	36	9	1	0
10	1	10	45	120	210	252	210	120	45	10	1
11	1	11	55	165	330	462	462	330	165	55	11
12	1	12	66	220	495	792	924	792	495	220	66
13	1	13	78	286	715	1287	1716	1716	1287	715	286
14	1	14	91	364	1001	2002	3003	3432	3003	2002	1001
15	1	15	105	455	1365	3003	5005	6435	6435	5005	3003
16	1	16	120	560	1820	4368	8008	11440	12870	11440	8008
17	1	17	136	680	2380	6188	12376	19448	24310	24310	19448

Interessante Punkte:

· Bezug zur Statistik: Die Zahlen einer Zeile nähern für große n eine Gaußsche Normalverteilung an. Diese kann natürlich wieder als Formel angenähert werden.

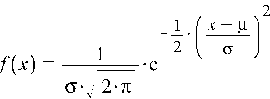
· Bezug zur Differentialrechnung: Die Differenzen über eine Spalte bilden immer wieder die gleichen Binomialkoeffizienten.

· Die Summe über eine Zeile ergibt immer 2^n. Man kann nachweisen, dass dies dadurch entsteht, dass die Funktion (x+y)^n mit x und y zwei Summanden hat. Für (x+y+z)^n ergibt sich entsprechend eine Summe von 3^n usw.

· Die Formel für die Faktoren "n über k" = n*(n-1)*(n-2)*... (n-(k-1)) / 1*2*3*...k

n=0 n=1 n=2 n=3 n=4

Rechenregeln für die Binomialkoeffizienten in der Tabelle mit Spalte m und Zeile n:

f[ m ][ n+1 ] = f[ m-1 ][ n ] + f[ m ][ n ] (4)

f[ m+1 ][ n ] = f[ m ][ n ] * (n-m) / (m+1) (5)

f[ 2 ][ n ] = f[ 1 ][ n ] * (n-1) / 2

f[ 3 ][ n ] = f[ 2 ][ n ] * (n-2) / 3

f[ 3 ][ n ] = f[ 2 ][ n ] * (n-3) / 4

In Gleichung (5) wird in einer Zeile n immer mit allen Faktoren 1..n multipliziert (n-m) wie auch dividiert (m+1). Dabei muss die Division immer aufgehen. Es muss also immer ein Faktor (m+1) enthalten sein. Betrachtet man die Formel für "n über k" dann erkennt man, dass die Binomialkoeffizienten in auffällig viele Primzahlen zerlegbar sind. Es existiert ein Bezug zu den Primzahlen.

Binomialkoeffizienten invertiert ermitteln

Man kann x^n – (x ± 1)^n auch immer auf kleinere Potenzen reduzieren. Symmetrisch dazu entstehen von oben nach unten beim Reduzieren auf eine kleinere Potenzen genau die gleichen Binomialkoeffizienten wie beim ausmultiplizieren von Potenzen.

n = m+1 = p+2 = q+3 = r+4; (6)

y:= x-1;

f:= x^n - y^n;

f:= x*x^m - x*y^m + y^m;

f:= x^2*x^p - x^2 * y^p + 2*y^p*x - y^p;

f:= x^3*x^q - x^3 * y^q + 3*y^q*x^2 - 3*y^q*x + y^q;

f:= x^4*x^r - x^4 * y^r + 4*y^r*x^3 - 6*y^r*x^2 + 4*y^r*x - y^r;

7. Die pythagoreischen Zahlentripel und Fermats letzter Satz

Pierre de Fermat hat behauptet, dass es für die Gleichung (7) keine ganzzahlige Lösungen für n>2 gibt. Der Beweis dazu war lange Zeit ein großes Problem der Mathematik. Erst über Symmetrien konnte 1994 Andrew Wiles einen Beweis erbringen.

x^n + y^n = z^n (7)

Für n=2 sind pythagoreische Tripel möglich, wenn über die 3te binomische Formel zwei Summanden entstehen. Wir stellen um, und Erweiterung über 3te binomische Formel:

y^2 = z^2 - x^2 = (z-x) * (z+x) (8)

Anschließend substituieren wir: x=u^2-v^2 y=2uv z=u^2+v^2

(2uv)^2 = (u^2+v^2-u^2-v^2) * (u^2+v^2+u^2-v^2) (9)

4 * u^2 * v^2 = (2*v^2) * (2*u^2)

Nach dem Vereinfachen sind beide Seiten der Gleichung gleich. Über die Variation von u und v können jetzt alle Tripel gefunden werden. Die Tripel sind dabei primitiv, wenn u>v und u,v teilerfremd und nicht beide ungerade sind. Primitiv heißt, dass die drei Zahlen nicht mehr durch einen gemeinsamen Faktor geteilt und so vereinfacht werden können (siehe auch Wikipedia).

Bei Fermats letzten Satz wird zuvor ausgeschlossen, dass Zahlen direkt auf beiden Seiten der Gleichung die gleichen Summanden besitzen können. Dies gilt, wenn x^n=0 oder y^n=0 oder alle 0 werden. Wir können jetzt die Gleichung (7) noch etwas umstellen. Es soll dabei deutlich werden, dass bei jedem Übergang die n-te Wurzel aufgehen muss, da ansonsten irrationale und somit chaotische Zahlen entstehen würden. Eine ganzzahlige Lösung ist dann nicht mehr möglich.

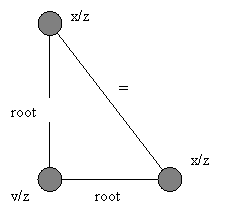
x/z = root[n] ( 1 – (y/z)^n ) (10)

y/z = root[n] ( 1 – (x/z)^n )

z/x = root[n] ( (y/x)^n + 1 )

y/x = root[n] ( (z/x)^n – 1 )

z/x = root[n] ( (y/x)^n + 1 )

z/y = root[n] ( (x/y)^n + 1 )

x/y = root[n] ( (z/y)^n – 1 )

z/y = root[n] ( (x/y)^n + 1 )

Ein Ansatz für einen Beleg von Fermats letzten Satz ist die Tatsache, dass unter Berücksichtigung der oben genannten Symmetrien maximal ein Polynom vom Typ (x±y)^2 wieder 2 Summanden aufweist. Für alle höheren Potenzen entstehen immer mehr als 2 Summanden:

(x+y)(x–y) = x² – y² (25)

(x±y)(x±y) = x² ± 2xy + y²

(x±y)(x±y)(x±y) = x³ ± 3x²y + 3xy² ± y³

(x+y)(x±y)(x–y) = x³ ± x²y – xy² ± (-y³)

(x+y)^2 * (x-y)^2 = x^4 – 2x²y² + y^4

(x+y)^5 = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5

Genau gesagt entstehen beim ausmultiplizieren von bei (x+y)^n mit einer ungeraden Potenz n insgesamt n+1 Summanden. Wenn genauso viele positive wie negative Faktoren vorhanden sind, entstehen n/2+1 Summanden.

Beweisansatz für Fermats letzten Satz:

1. Alle Zähler und Nenner unter den Gleichungen (10) werden mit n potenziert, ergeben daher n-te Potenzen.

2. Außerdem wird aus allen Brüchen+1 die n-te Wurzel gezogen. Wäre die Lösung nicht rational, also keine n-te Potenz, dann wäre die Wurzel irrational und könnte somit nicht ganzzahlig werden.

3. Alle Brüche können immer so mit dem Nenner multipliziert werden, dass wieder ganze Zahlen entstehen.

4. Bei einer Multiplikation werden immer alle Summanden mit allen Summanden multipliziert (a+b)(c+d)=ac+ad+bc+bd. Es wird eine unabhängige Symmetrie erzeugt.

5. Nur maximal für n=2 kann für die n-te Potenz unter der Berücksichtigung der möglichen Variationen aufgrund von Symmetrien eine Form entstehen, in der nur zwei Summanden entstehen.

6. Eine mögliche ganzzahlige Lösung kann nur bei gleichen Faktoren entstehen, nicht aber bei einer neuen Symmetrie. Nur die Linearkombinationen z^2 - x^2 = (z-x) * (z+x) liefert Lösugen. Daher können wir annehmen, dass es keine Lösungen gibt, die wir noch nicht berücksichtigt haben.

7. Wenn bei dem "Euler Brick" auch noch sqrt( a^2+b^2+c^2 ) ganzzahlig sein soll, haben wir eine weitere Linearkombination. Eine Lösung ist nicht mehr möglich.

8. Freiheitsgrade einer Gleichung

Welche Variationen kann eine Gleichung grundsätzlich enthalten?

Grad=0: a=0 a=1 … (26)

Grad=1: a=b a=b+1 a=1/b …

Grad=2: a=b+c a=b+c+1 a=b/c a=b*c …

Versuchen wir anders herum etwas Allgemeines immer weiter einzuschränken. Wir können dabei eine Variable einer Funktion auf 1 setzen oder mit einer anderen Variable gleich setzen.

Grad=4: (a+c)(b+d) = ab + ad + cb + cd alles ist frei wählbar (27)

Grad=3: (a+c)(b+1) = ab + a + cb + c mit d=1

Grad=2: (a+c)(b+d) = ab + cd mit (c=d und a=-b) oder (c=-d und a=b)

Grad=2: (1+c)(1+d) = 1 + c + d + cd

Grad=1: (1+c)(1+d) = 1 + cd mit c=-d

Grad=0: (1+1)(1+1) = 1 + 1 + 1 + 1 keine freien Variablen

Mit kleiner werdenden Freiheitsgraden vereinfacht sich die Gleichung immer weiter. Da die ausmultiplizierte Gleichung immer alle Kombinationen enthält, heben sich nach der Reduktion um einen Freiheitsgrad entweder 0, 1 oder 2 Summanden auf. Dies sollte auch für höhere Potenzen wie z.B. der Funktion (28) gelten.

(a+d+g)(b+e+h)(c+f+i) = abc + abf + abi + aec + aef + aei + ahc + ahf + ahi (28)

+ dbc + dbf + dbi + dec + def + dei + dhc + dhf + dhi

+ gbc + gbf + gbi + gec + gef + gei + ghc + ghf + ghi

9. Eulersche Vermutung

Es gibt Gleichungen, die sich komplett auflösen a-a=0 oder a/a=1. Wenn sich nicht alle Elemente auslöschen, dann kürzt sich bei symmetrischen Kombinationen maximal die Hälfte aller Elemente raus. Für (a+b)^n entstehen immer n+1 Summanden. Werden diese mit der gespiegelten Variante verknüpft, (a+b)^n + (a-b)^n so löschen sich durch die Symmetrie die Hälfte der Faktoren aus.

Euler hat vermutet, dass es für die Gleichung (29) keine Lösung gibt. Dies hat sich als falsch rausgestellt.

a₀^n + a₁^n + a₂^n + ... = a_m^n mit m=n (29)

Trotzdem können nun einige Annahmen gemacht werden. Die Gleichung sollte dazu noch einmal in symmetrischere Formen gebracht werden.

a₀^n + a₁^n + a₂^n + ... + a_m^n = 0 (Annahme, dass alle a_x ungleich sind)

(a₀/a_m)^n + (a₁/a_m)^n + ... (a_m-1/a_m)^n = -1 (Ein Summand kann aufgelöst werden)

Aufgrund von Symmetrien kann man sagen, dass es keine Lösung für m<n/2 bzw. m<(n+1)/2 für ungerade n gibt. Nur für Gleichungen mit m>n wird sicher eine Lösung existieren. Der Bereich dazwischen muss im Moment noch als chaotisch angesehen werden.

Lösungen in Tabellenform:

N=	0	1	2	3	4	5	6	7	8	9	x^0, x^1, x^2, ....
m=
1	+										1=1 trivial
2	+	+–	–	–	–	–	–	–	–	–	a^2 = a^2 Ausschluss gleicher Zahlen
3	+	+	+	–	–	–	–	–	–	–	Ausschluss komplexer Zahlen
4	+	+	+	+	+	–	–	–	–	–	Ausschluss von a^n + b^n = a^n + b^n
5	+	+	+	+	+	+	?	–	–	–	...
6	+	+	+	+	+	+	?	?	?	–
7	+	+	+	+	+	+	+	?	?	?
8	+	+	+	+	+	+	+	+	?	?
9	+	+	+	+	+	+	+	+	+	?
10	+	+	+	+	+	+	+	+	+	+

Bekannte Lösungen:

3^2 + 4^2 = 5^2 (3 Elemente)

1^3 + 6^3 + 8^3 = 9^3 (4 Elemente)

95800^4 + 217519^4 + 414560^4 = 422481^4 (4 Elemente)

30^4 + 120^4 + 272^4 + 315^4 = 353^4 (5 Elemente)

27^5 + 84^5 + 110^5 + 133^5 = 144^5 (5 Elemente)

Wenn wir die Funktion x² + y² = z² quadrieren, erhalten wir x^4 + 2 x^2 y^2 + y^4 = z^4. Dazu gibt ganzzahlige Lösungen der Form 2x^4 + y^4 + 2z^4 = a^4 (Beispielsweise 2^4 + 2^4 + 3^4 + 4^4 + 4^4 = 5^4) die ähnliche symmetrisch Form ausweisen. Vermutlich gilt dies auch für höhere 2-er Potenzen wie 8, 16, 32, ...

Im schlechtesten Fall werden für eine um 1 höhere Potenz doppelt so viele Summanden benötigt. Die Anzahl der Summanden m hängt in dem Fall direkt mit der Potenz n über m=2^n zusammen.

2^0 = 1 = 1 (30)

2^1 = 2 = 1+1

2^2 = 4 = 1+1+1+1

2^3 = 8 = 1+1+1+1 + 1+1+1+1

2^4 = 16 = 1+1+1+1 + 1+1+1+1 + 1+1+1+1 + 1+1+1+1

Bei eine Potenzfolge einer n-ten Potenz kann man n mal eine Differenzfolge d_n = a_n+1 – a_n bilden, bis alle Elemente der Folge einen konstanten Wert von n! annehmen (Bezug Fakultät zu Binomialkoeffizienten). So wird im besten Fall durchschnittlich nur ein zusätzlicher Summand für eine um 1 erhöhte Potenz benötigt. Ähnlich wie bei den 2er-Potenzen 2^n, kann mit einer zusätzlichen Zahl der mögliche Zahlenbereich jeweils verdoppeln werden.

10. Bezug N≠NP

Wenn 2 gleich große Listen miteinander vereint werden und die Zuordnung zu den ursprünglichen Liste dabei verloren geht, dann dauert die Suche nach einem Element bei sortierten Listen einen Iterationsschritt länger (binary search) und bei nicht sortierten Listen doppelt so lange (linear search). N≠NP gilt also, sobald Informationen verloren gegangen sind. (Zumindest sollte das für die Primfaktorzerlegung gelten.) Erst in einem abgeschlossenen System, in dem keine Information verloren geht, wird N=NP.

11. Traveling Salesman Problem (vom 03.10.2012)

Der Abstand im 2D-Raum zu einem anderen Punkt wird durch unendlich viele Punkte auf einem Kreis definiert. Sehr kleine Verschiebungen können dazu führen, dass es eine andere optimale Lösung gibt. Für die Lösung eines Teilabschnitts können beliebige Kombinationen zusammengelegt werden. Beides führt dazu, dass eine optimale Lösung in einer chaotischen Struktur gefunden werden muss. Beispiele können zeigen, dass auch sehr lange und eher unwahrscheinliche Strecken berücksichtigt werden müssen. Wenn allerdings die längste Strecke Teil der optimalen Lösung ist (z.B. L-Form), dann kann die nächst kürzere Strecke nicht die 2t-längste Strecke sein. Es sind also Vereinfachungen möglich (Siehe auch O-Form, X-Form, #-Form, ...)

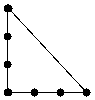
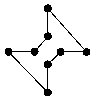
Aufgrund der sehr einfachen und symmetrischen Aufgabenstellung muss die optimale Lösung für eine Worst-Case-Laufzeit auch eine einfache Struktur aufweisen. Aufgrund der trotzdem vorhandenen chaotischen Struktur muss mindestens eine exponentielle Laufzeit gegeben sein. Aufgrund möglicher Vereinfachungen und des logischen Bezugs zwischen Fakultäten 1*2*3*...n und Exponentialfunktionen n*n*n*n, ... , ist die exponentielle Laufzeit im 2D-Raum vermutlich richtig, aber aufgrund der chaotischen Strukturen grundsätzlich nur indirekt über Symmetrien beweisbar.

Aus einer maximal chaotischen Struktur kommt man immer nur durch die Umkehrfunktion oder eine symmetrisch äquivalenten Funktion wieder in den nicht chaotischen Bereich.

12. Bezug Riemansche Vermutung

Die Zeta-Funktion ζ(s) = Sum( 1/n^s, n=1..infinity ) hat aufgrund seiner komplexen Zahl 2 Freiheitsgrade (2D-Fläche). Nun bilden auch unendlich viele parallele Linien eine Fläche. Man kann sich nun vorstellen, dass alle Linien zu einer langen Linie hintereinander gekettet werden und auf eine Kreisbahn gekrümmt werden (Bezug komplexe Zahlen). Aufgrund der Möglichkeit verschiedener Anzahl von Umrundungen des Kreises ergibt sich ein Bezug zu Primzahlen (Der Primzahlenbezug konnte mathematisch belegt werden). Alle Nullstellen bleiben so auf dem Kreis oder entsprechend dazu auf der kritischen Geraden der Zeta-Funktion (Re=1/2). Da es keine weiteren Freiheitsgrade gibt, gibt es auch keine Möglichkeit für weitere Nullstellen. Durch die einfache Form der Funktion kann man auch „versteckte“ Lösungen ausschließen. (Mathematisch sicherlich unvollständig, aber die Struktur von Mustern sollte deutlich werden.)

13. Fourier-Transformation

Die Fourier Analyse F(f)(t) = 1 / (2*p)^(n/2) * Int( f(x) * exp( -i*t*x), x ) ist ein schönes Beispiel für Symmetrie. Aufgrund der Tatsache, dass ein Kreis unendlich viele Symmetrien besitzt, wird diese Transformation erst möglich. Allerdings müssen im Normalfall schon unendlich viele Schwingungen überlagert werden, um ein Signal exakt abzubilden. Die Transformation ist dabei so etwas wie eine Invertierung der Funktion. Aus unendlich vielen symmetrischen Funktionen kann man eine bestimmte (oder auch jede beliebige) unendlich komplizierte Funktion abbilden.

Symmetrien der Kettenbrüche

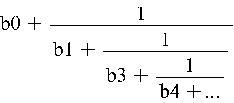
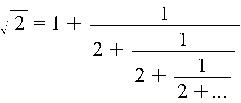
Es konnte gezeigt werden, dass es eine Kettenbruchentwicklungen für die Quadratwurzel einer beliebigen ganzen Zahl d existiert, wobei der Kettenbruch zwar nicht endlich ist, die Koeffizienten b0, b1, b2, b3, ... aber immer periodisch sind. Bemerkenswert ist, dass die Periode zwischen 2 Quadratzahlen immer mit 2 mal der erste Quadratzahl endet. Die anderen Koeffizienten werden dabei zunehmend chaotischer.

Kettenbruchentwicklung von sqrt(d)

1 [1]

2 [1; 2]

3 [1; 1; 2]

4 [2]

5 [2; 4]

6 [2; 2; 4]

7 [2; 1; 1; 1; 4]

8 [2; 1; 4]

9 [3]

10 [3; 6]

11 [3; 3; 6]

12 [3; 3; 6]

13 [3; 1; 1; 1; 1; 6]

14 [3; 1; 2; 1; 6]

15 [3; 1; 6]

16 [4]

17 [4; 8]

Die Brüche aus aufeinanderfolgenden Fibonaccizahlen {1,1,2,3,5,8,13,21,34,55,89,144,...} führen übrigens stets auf Kettenbrüche der Form (1,1,1,1,...,1,1,2), bzw. (0,1,1,1,...,1,1,2) je nachdem, welche Zahl im Zähler bzw. im Nenner steht. Der Zahlenwert der Quotienten nähert sich sehr rasch dem goldenen Schnitt an. Dieser hat die bemerkenswerte unendliche Kettenbruchentwicklung (1,1,1,1,1,1,1,1,...).

14. Primfaktorzerlegung

Beim Bezug der Primfaktorzerlegung, werden genau die Lücken gesucht, die keine Faktoren aufweisen und daher Primzahlen sind. Angenommen (m+1) ist ein Primfaktor einer Zahl, f[ m-1 ][ n ] ist das Produkt der restlichen Primfaktoren und (n-m+1) ist 1. Wir wissen, dass n=m ist. Wenn wir f[ 1 ][ n ] = n kennen würden, wüssten wir wie n und damit auch m aussieht. Wir müssen also rückwärts f[ 0 ][ n ] = 1 bestimmen.

f[ m-1 ][ n ] = f[ m ][ n ] * (m) / (n-m+1)

f[ m-2 ][ n ] = f[ m ][ n ] * (m) / (n-m+1) * (m-1) / (n-m+2)

f[ 0 ][ n ] = [ (m)*(m-1)* (m-2)*... ] / [ (n-m+1)*(n-m+2)*(n-m+3)*... ]

f[ 0 ][ n ] = 1 führt leider zu keiner Lösung!

Auch eine iterative Lösung, bei der man schrittweise versucht mit 2 Faktoren immer näher an die zu faktorisierende Zahl heranzukommen, funktioniert nicht, da sich Primzahlen grundsätzlich chaotisch verhalten. Scheinbar gibt es wirklich keine effiziente Lösung für das Zerlegen in Primfaktoren. Die Tatsache, dass in der Kryptographie nur 2 Primzahlen miteinander multipliziert werden, macht die Sache nicht einfacher, da daher auch kein Faktor abgespalten und so etwas vereinfacht werden könnte?

Die chaotische Struktur von Primzahlen kann damit begründet werden, dass immer kompliziertere Primzahlen bezogen auf ihr Zahlenmuster für die Existenz oder Nichtexistenz von noch komplizierteren Primzahlen verantwortlich sind.

15. Symmetrien von Potenzen in verschiedenen Zahlensystemen

In jedem beliebigen System (bis auf Binärsystem) gilt:

10^2 =100 und (10+1)^2 = 121 Abstand ist 20+1

100^2 =10 000 und (100+1)^2 = 10201 Abstand ist 200+1

1000^2=1 000 000 und (1000+1)^2=1 002 001 Abstand ist 2000+1

Umgekehrt gilt für alle Systeme (bis auf Binärsystem):

10^2 =100 und (10-1)^2 = 100-20+1 Abstand ist 20-1

100^2 =10 000 und (100-1)^2 = 10 000-200+1 Abstand ist 200-1

1000^2=1 000 000 und (1000-1)^2=... Abstand ist 2000-1

(10+1)* (10+1) = 121 (Systeme größer 2)

(10+1)* (10+1)* (10+1) = 1331 (Systeme größer 3)

(10+1)* (10+1)* (10+1)* (10+1) = 14641 (Systeme größer 6)

(10+1)* (10+1)* (10+1)* (10+1)* (10+1) = 15AA51 (Systeme größer 10)

(10-1)* (10-1) = 100-20+1 (Systeme größer 2)

(10-1)* (10-1)* (10-1) = 1000-300+30-1 (Systeme größer 3)

(10-1)* (10-1)* (10-1) * (10-1) = 10000-4000+600-40+1 (Systeme größer 6)

Das Zahlensysteme sehr symmetrische Strukturen sind, zeigt sich auch darin, dass Zahlensysteme gemischt werden können. Für jede Stelle kann Beispielsweise ein anderes Zahlensystem verwendet werden. Wir zählen dann z.B. so:

0, 1, 10, 11, 20, 21, 30, 31, 100, 101, 110, 111, 120, 121, 130, 131, 200, ...

16. Anhang Binomialkoeffizienten für (x+1)^61

Muster für jede Potenz und in jedem Zahlensystem (außer Binärsystem)

(10+1)^2 = 100+20+1 = 121 (10-1)^2 = 100-20+1

(1+0,1)^2 = 1+0,2+0,01 = 1,21 (1+0,1)^2 = 1-0,2+0,01

m und n sollen zueinander die Umkehrung von Potenz und Wurzel liefern.

m*n = 1

a = ( b + 1 )^n

a^m = b + 1

b = a^m – 1

Potenzen x^2 sind besondere Multiplikationen a*b und damit invertierbar

In einer Reihe wird b mal a addiert, beziehungsweise in einer Spalte a mal b addiert. Auch nachfolgende Funktion muss somit invertierbar sein:

(a+b)(b+d) = ab + ad + cb + cd

Beweisansatz für Symmetrien

Für (z/y)^n = (x/y)^n + 1 nehmen wir an, dass die z/y und x/y als rationelle 2 Dimensionale Fläche aufgefasst werden kann. Es gibt aber nur für bestimmte Punkte die „einrasten“ können Lösungen. Würde man die Gleichung noch weiter einschränken, so können keine Lösungen mehr möglich sein. Mit z=x würde (x/y)^n = (x/y)^n + 1 folgen, was unwahr ist. Die 1 ist so quasi ein halber Freiheitsgrad.

17. Symmetrie der Mathematik

Aufgrund von chaotischen Teilen, können viele Probleme prinzipiell nicht arithmetisch bewiesen werden. Dazu gehört z.B. bestimmte Kettenbrüche, aber auch andere chaotische Probleme wie die Primzahlenverteilung, Fermats letzter Satz, die Riemansche Vermutung, usw.. Eine Existenz von Mustern kann nur aufgrund von Symmetrien belegt werden. Die Mathematik sollte daher zwischen einem:

· arithmetischen Beweis (über eine mathematische Formel) und über einen

· transzendenten Beweis (Rechnen mit Unendlichkeiten) unterscheiden.

· Unsere Welt ist also eine Welt der Informationen, des Chaos, der Symmetrien, der Teilchen, der Wellen, der Hierarchien, der Emergenz, der Fraktale und vielleicht sogar alles gleichzeitig und genauso wieder nichts von Allem. Und vermutlich ist unsere Welt es auch, obwohl wir Menschen es manchmal nicht wahr haben wollen.

· Es macht Sinn zu definieren, dass es genauso viele Symmetrien gibt, wie es auch Abhängigkeiten gibt. Die Hälfte kann berechnet werden. Die andere Hälfte existiert einfach. Es muss außerdem genauso viele Verbindungen wie Knoten geben. Alles muss aus Symmetriegründen austauschbar sein.

· Wenn sich n Objekte mit n Objekten in der Fläche austauschen, dann hat man n^2 Verbindungen. So sind Dimensionen definiert.

· Alle mathematischen Probleme, die über unendliche Reihen laufen, können nur aufgrund von Symmetrien bewiesen werden (Annahme, dass es Dimensionen gibt). Die Weltformel kann sicherlich im Extremfall über Symmetrien in einem unendlich-Dimensionalen Raum bestimmt werden. So eine Struktur kann ALLES beweisen.

· Aus dem vollständigen Chaos kommt man nur mit der Umkehrfunktion (Quadrieren nach Wurzel) oder durch eine symmetrisch äquivalente Funktion wieder raus.

· Im Fall, dass eine endliche Anzahl an Zuständen im Universum gibt, dann würde man erwarten, dass man all diese Zustände möglichst genau bewertet, um eine optimale Lösung zu finden. In einem fraktalen Universum gibt es aber in allen Dimensionen unendlich viele Zustände, was dazu führt, dass es prinzipiell unmöglich ist, auch nur irgendetwas zu bewerten. Alles ist vorherbestimmt.

· Information ist das Fundamentalste, was auf der Welt existiert.

· Information ist im Universum absolut zufällig verteilt. Aber aufgrund dieses zufälligen Ungleichgewichts musste der Mensch dann zwangsweise entstehen.

· Zwischen Relativitätstheorie und Quantenphysik existiert ein unendlich chaotisches Chaos. Die einzige Symmetrie ist die Schnittstelle zu den beiden Theorien.

· ALLE Strukturen sind gleichzeitig chaotisch und symmetrisch.

· Mit Chaos kann man nicht rechnen.

· Ein Beleg dafür sind die Taylor-Reihen. Addiert man die Reihen von sin(x) und cos(x) ohne auf die Vorzeichen zu achten, dann ergibt sich exp(x) was einen Bezug zum Unendlich-Dimensionalen-Raum herstellt. exp(2) =2D, exp(3)=3D, ...

· Zu jeden Zustand gibt es einen Gegenzustand und zu jedem Übergang einen inversen Übergang. Es gibt immer die Möglichkeit, aus einem richtigen Zustand in einen falschen Zustand zu wechseln. Und aus dem falschen Zustand kommt man immer wieder mit einem 2ten Zustandswechsel wieder in einen richtigen Zustand. Wenn das Universum fraktal ist, dann kann über binäre Informationen maximal die Hälfte des Universums beschrieben werden. Der Rest muss chaotisch bleiben. Auch bei "realen" 3-dimensionalen Körpern führt die fraktale Oberfläche dazu, dass sogar hier Chaos existiert.

o 1+2=3 (richtig)

o 1+3=3 (falsch)

o 1+3=4 (richtig)

18. Wieso ist unsere Welt 3-dimensional?

Der Mensch sieht und versteht aufgrund seiner Augen maximal 2-D Strukturen. Auch das Hören und Fühlen beruht nicht auf 3-D Strukturen. Erst mit einer zusätzlichen Dimension wie der Zeit schaffen wir es ein 3-D Strukturen zu erfassen. 4-D Strukturen können wir uns nur über einen mathematischen Formalismus Vorstellen. Die Quantenmechanik nutzt dazu die Furier Analyse und die Relativitätstheorie arbeitet mit dem Werkzeug der Raumverzerrung (Hermann Minkovski-Diagramme).

Das Demo PhysicsWave.exe soll einige Eigenschaften des 3-D Raumes verdeutlichen. Selektiert man „Bending“ und initialisiert man mit „Init“, dann sieht man einen Würfel aus Linien. Über ziehen mit der Maus kann man den Würfel rotieren und verschieben. Mit der „Space“-Taste kann man die Ansicht auf eine bestimmte Seite einrasten.

Wenn man sich alle 6 Seiten ansieht, dann erkennt man, dass alle Seiten bis auf Spiegellungen gleich aussehen. Dies wurde durch eine Rotation der Linien um die 3 Raumachsen erreicht.

Außerdem erkennt man, dass immer die 2 gegenüberliegenden Ecken des Würfels das gleiche Muster aufweisen. Der Versuch, allen Ecken das gleiche Muster zu geben führt immer dazu, dass nicht mehr alle 6 Seiten des Würfels identisch aussehen. Genauso wie eine Rotation im 2-D Raum immer das ganze Objekt beeinflusst, gibt es auch hier im 3-D Raum bestimmte Abhängigkeiten.

Bei höherdimensionalen Strukturen entstehen immer neue und chaotischere Muster. Die Penrose-Parkettierung mit ihren dualen Fliesenformen ist ein schöner Beleg dafür, wie schon in einem 2-D Raum chaotische Strukturen entstehen können.

Genau gleichwertige ist aber auch die Aussage, dass Planetenbahnen ab dem 3. Himmelskörper chaotisch werden, was ebenfalls eine Begründung für unseren 3-D Raum darstellt. (Siehe dazu auch unter Stabilität in einer 3-Parteien-Demokratie.) Es existiert eine Dualität der Wahrheit der beiden Aussagen.

· Gleichwertigkeit wird im Welle-Teilchen-Dualismus deutlich.

· Physikalische Kräfte können genauso als (Austausch-) Teilchen angesehen werden.

restart;

#*********************************************************

# Ganzzahlige Lösungen für a1^n + a2^n + ... = am^n

#*********************************************************

FindEqu:=proc( sum

, min::integer

, max::integer

, exp::integer

, depth::integer

, maxdepth::integer

, tab::Array ) local x,y;

if depth = maxdepth then

for y from min to max do

if sum = y^exp then print('Lösung',tab,y); fi;

#print( sum, tab, y ); #debug

end do;

else

for x from min to max do

if depth = 0 then print(x); end if;

tab[depth+1] := x; #set

FindEqu( sum+x^exp, x+1,max, exp, depth+1,maxdepth, tab );

tab[depth+1] := 0; #set back

end do;

fi;

end proc:

tab := Array([0,0,0,0,0]):

#FindEqu(0, 1, 30, 2, 0, 2, tab ): #Pythagroreische Tripel

#FindEqu(0, 27, 150, 5, 0, 4, tab ): #Bezug Eulersche Vermutung

#*********************************************************

# Eine Zahl als Summe von Binomimalkoeffizienten

#*********************************************************

SearchSum:=proc( number::integer,

sum::integer,

depth::integer,

exp::integer,

tab::Array,

solution::Array ) local x,y;

if sum = number then

print('Lösung',solution);

else

if depth<=exp then

for x from 1 to exp/2+1 do

solution[depth] := tab[x];

SearchSum( number, sum+tab[x], depth+1, exp, tab, solution );

solution[depth] := 0;

end do;

fi;

end proc:

#*********************************************************

# Faktoren des ausmultiplizierten Polynoms (x+1)^n

#*********************************************************

PolyFactors:=proc( exp::integer )

local solution,x,y, tab::Array;

tab := Array( 1..exp );

tab[1] := 1; #Initalisieren

for y from 1 to exp do

for x from exp by -1 to 2 do

tab[x] := tab[x-1] + tab[x];

end do;

for x from 1 to exp/2+1 do print( tab[x] ); end do;

for x from 1 to exp/2+1 do print( ifactor( tab[x] ) ); end do;

# print( tab );

# for x from 1 to 33 do

# print( "Zahl",x );

# solution := Array( 1..exp );

# SearchSum( x, 0, 1, exp, tab, solution );

# end do;

end proc:

PolyFactors( 61 ):

g := expand( (x+1)^61 );

expand( (x+y)^3*(x-y)^3 );

expand( (x+y)^7 + (x-y)^7 );

expand( (x+y)^7 - (x-y)^7 );

convert(6^3, base, 6);

convert(6^3*8^3, base, 6*8);

root[3](512); root[3](512000); root[3](512000000);