Das fraktale Weltbild

Die Wissenschaft hat viele Erkenntnisse aus Experimenten erlangt und wichtige Überlegungen auf den Weg gebracht. Trotzdem hat es bis heute niemand geschafft diese Vielzahl an Theorien zu vereinheitlichen oder zumindest in eine symmetrische Struktur zu verpacken. Alles weist darauf hin, dass unser Universum daher nicht mit Mustern bis ins kleinste Detail beschreibbar ist.

Die Wissenschaft kennt viele chaotische Strukturen:

Die Mathematik kann relativ einfach beweisen, dass die Wurzel aus 2 irrational und somit zum Teil chaotisch ist. Anders herum ist die Natur unsere Erde so voller Muster und Symmetrien. Wieso kennt also die ausschließlich auf Logik aufgebaute Mathematik das Chaos und wieso ist die absolut freie Natur so voller Muster und Symmetrien? Die Wissenschaft hat dazu 2 Begriffe:

Die Emergenz bezeichnet Muster, die quasi aus dem Chaos entstehen. Ein Beispiel ist ein Wirbelsturm, der aus so etwas chaotischem wie Wetterstrukturen entsteht und trotzdem immer eine ähnliche Struktur aufweist.

Fraktale Muster wie die Mandelbrotmenge zeigen, dass auch sehr einfache mathematische Formeln zu sehr eleganten und komplexen Mustern fähig sind. Fraktale beinhalten chaotische und auch symmetrische Komponenten zu gleichen Teilen.

Ist unser Weltbild auch fraktal und emergent?

Mathematik:
·       Linearität (Zahlenstrahl)
·       Complexe Zahlen (Schleifen und Kreissymmetrien)
·       Irrationale Zahlen (chaotische Systeme)
·       Binomialkoeffizienten und Fibonacci-Folge
·       Symmetrien und Ähnlichkeiten (absolut oder relativ)
·       Kegelschnitte: Hyperbel, (speziell 1/x), Kreis, Ellipse undParabel
·       Unendliche Reihen und Folgen, Kettenbrüche
·       Taylor-Reihen für e^x, sin(x), cos(x), ln(x)
·       Integrale und partielle Ableitungen und die Gaußsche Normalverteilung
·       Faltung (f*g)(t) = 1/T * Int( f(tau) * g(t-tau), a..a+T)
·       Sphärische und hyperbolische Geometrie
·       Elliptische Kurve (x^2 = x^3 + ax + b)

Logik und Muster:
·       Ziegenproblem (Monty-Hall-Problem)
·       Junge-oder-Mädchen-Problem
·       Gefangenenparadoxon (three prisoners problem)
·       Ententest (Ducktest)
·       Symmetrien versus Asymmetrien
·       Penrose-Parkettierung
·       Realität und 3D-Raum

Physik:
·       Kräfte und Balancen (Hebelgesetz)
·       Larmor-Präzession
·       Keplersche Gesetze
·       Fouriertransformation (Invertierung von Systemen)
·       Schwingungen, Wellen und Interferenzen
·       Hauptsätze derThermodynamik
·       Fermat's principle of least time
·       Doppelspalt-Experiment (Welle-Teilchen-Dualismus)
·       Lichtgeschwindigkeit (Michelson-Moorley-Experiment)
·       Relativitätstheorie (Minkowski-Diagramme)
·       Quantenphysik (Vielfalt der Feynman-Diagramme)
·       Welle-Teilchen-Dualismus und Komplementaritätsprinzip
·       Chaostheorie (Feigenbaum-Diagramm)
·       Quantenfeldtheorie und Quantenchromodynamik
·       Zeitdilatation der SRT (Myonen-Experiment)
·       Bellsches Raumschiffparadoxon und Zwillingsparadoxon
·       Bellsche Ungleichungen
·       Supraleitung und Bose-Einstein-Kondensat (BEC)
·       Casimir-Effekt und das unendlich Kleine
·       Tscherenkow-Strahlung, Lamb-shift
·       Coulombpotential in Galaxien
·       Die Sichtweise der Dekoherenz
·       Schrödingergleichung
·       String-Theorie und Lie Gruppe (E8)

Informatik:
·       Der Maxwellsche Dämon verbindet Information und Energie
·       Formale Sprachen (als Abgrenzung von natürlichen Sprachen)
·       Komplexität von Softwarestrukturen
·       Hierarchien und Baumstrukturen
·       Rekursionen und Search-Algorithmen
·       Gödels Halteproblem und Unvollständigkeits-Satz der Arithmetik
·       „Das Ganze ist mehr, als die Summe seiner Einzelteile“
·       Kreis-Ellipse-Problem
·       Object-relational impedance mismatch (Unverträglichkeit von relationalen Datenbanken und objektorientierter Programmierung)
·       Liskovsche Substitutionsprinzip (LSP) oder Ersetzbarkeitsprinzip
·       Interface-Segregation-Prinzip,
·       Dependency-Inversion-Prinzip
·       Law of Demeter (LoD - Gesetz von Demeter)
·       Design by Contract (Entwurf gemäß Vertrag)
·       Encapsulation (Datenkapselung)
·       Linguistic-Modular-Units-Principle (Prinzip linguistisch-modularer Einheiten)
·       Self-Documentation Principle (Selbstdokumentierungsprinzip)
·       Uniform Access Principle (Prinzip des gleichartigen Zugriffes)
·       Single-Choice-Principle
·       Persistence-Closure-Principle
·       Reuse-Release-Equivalence-Principle
·       Common-Closure-Principle
·       Common-Reuse-Principle
·       Acyclic-Dependencies-Principle
·       Stable-Dependencies-Principle
·       Stable-Abstractions-Principle
·       Lambdakalkül (eindeutigere Beschreibung eines Systems)
·       Single Responsibility Principle
·       Open-Closed Principle
·       Interface Segregation Principle

Strukturen des Denkens:
 ·       6 (Denk-)Hüte-Prinzip (Analytisch, Emotional, Kritisch,Optimistisch, Kreativ, Ordnend)
·       Keep it Simple Stupid
·       You “Ain’t Gonna Need It
·       Problem und Zielorientiert

Menschliche Strukturen:
 ·       Choleriker, Sanguiniker, Melancholiker, Phlegmatiker
·       Medizin und Placeboeffekt
·       Genotyp und Phänotyp (Erbbild versus Menge aller Merkmale)
·       Evolutionstheorie („Black Smoker“, Gradualismus und Punktualismus)
·       Gene, Chromosom, DNA, Proteine, Intron, Exons, Transpons,
·       Paradoxien und optische Täuschungen
·       Psychosen und bipolare Störungen
·       Hypochonder, Tourett-Syndrom, ...

Gesellschaftliche Strukturen:
 ·       Spieltheorie
·       Religionen, Kommunismus und Nationalsozialismus
·       Demokratie und Anarchie ( Auge um Auge )
·       Recht und Unschuldsvermutung
·       „Unwissenheit schütz vor Strafe nicht“
·       Peter-Prinzip (Hierarchische soziale Strukturen)
·       Tocqueville-Effekt
·       Braindrain

Chaostheorie
 ·       Logistische Gleichung: x(n+1) = r * x(n) * ( 1 - x(n) )  (n=Iteration, r=System)
·       Fraktale und selbstähnliche Strukturen (Mandelbrotmenge)
·       Ray-Tracing

Die Vorstellung eines Fraktalen Universums

Die unten gezeigte Struktur zeigt eine doppelt hierarchische und multi-symmetrische Struktur. Aber hat so eine symmetrische Struktur etwas mit unserer schwingenden und verzerrten Welt gemeinsam? Die Fourier-Transformation besagt, dass ALLE Kurvenformen über die Addition einer endlichen Zahl an Sinusschwingungen nachgebildet werden können. Dies ist möglich, da der Kreis die einfachste geometrische Figur ist, die unendlich viele Symmetrieachsen besitzt?

 

 

 

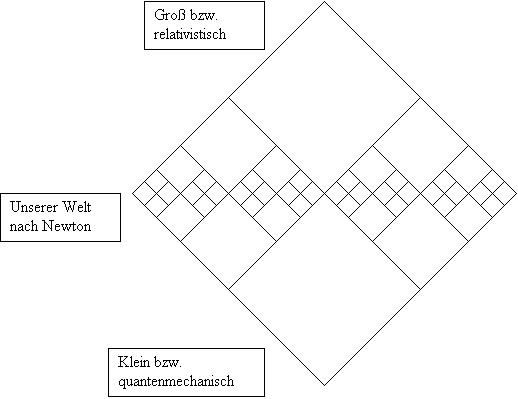
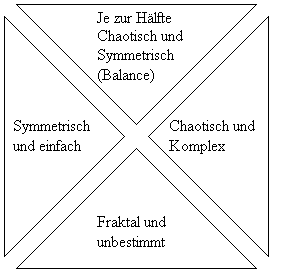
Fraktal heißt, dass gleichzeitig ALLES Symmetrisch ist und genauso auch ALLES chaotisch ist. Gleichzeitig ist ALLES berechenbar und außerdem gibt es Balancen die einfach definiert werden müssen. Das ist die einfachste Darstellung unseres Universums. Wer es nicht glaubt, der sollte selber einmal alle Zustände durchrechnen.

Das Diagramm selber ist auch wieder fraktal. Es ist symmetrisch aufgebaut, hat aber die chaotische Komponente der willkürlichen Gegenüberstellung von beliebigen Symmetrieeigenschaften. Die Sprache kann dabei wieder als fraktal bezeichnet werden.

Kann die Wissenschaft maximal die Hälfte aller existierenden Symmetrien in Modellen beschreiben? Existieren viele Dinge nur, weil wir sie untersuchen? (Wirtschaftssysteme oder auch Softwaresysteme) Stellt das Konstrukt der Physik oder Mathematik selber wieder eine fraktale Struktur dar? So wie es aussieht ist unser Universum, die Natur, der Mensch und seine Gesellschaftsstrukturen fraktal.

Ist es daher unentscheidbar, ob die Vereinigung der Quantenphysik und Relativitätstheorie maximal einfach 1=1 (Logik) oder endlich lösbar (Physik) oder unendlich kompliziert (Mathematik), oder prinzipiell unlösbar ist (Philosophie)?

Symmetrien versus Chaos

Wenn man alle Dinge mit Symmetrien beschreiben möchte, dann benötigt man unendlich viele dieser Symmetrien (Informationsproblem). Die Formel 1+1=2 ist sicherlich aufgrund der mathematischen Symmetrien richtig. Wird jetzt eine Zahl verändert, dann ist das Ergebnis sicherlich falsch. Die Formal kann anschließend nur über eine einzige „richtige“ Veränderung wieder korrigiert werden. Wenn nun ein falsches Ergebnis als Chaos „definiert“ wird und ein richtiges Ergebnis als Symmetrie „definiert“ wird, dann darf man behaupten, dass unser Universum exakt zu gleichen Teilen aus Chaos und Symmetrien besteht. Oder sollten wir doch eher behaupten, dass 1/3 symmetrisch ist, 1/3 chaotisch und 1/3 Definition? Vermutlich ist beides sowohl falsch als auch richtig.

Die Definition von Chaos:

Wie viel Informationen benötigt eine Formel mindestens, um die unten gezeigte Struktur komplett zu beschreiben? Es kann gezeigt werden, dass es einige Symmetrien gibt, die auf Vereinfachungen und einen geringen Informationsgehalt hindeuten.

 

 

 

Wir können mit Gleichungen vieles beschreiben. Trotzdem gibt es Grenzen. Dies liegt in der Tatsache, dass auch eine Gleichung beschrieben werden muss. Außerdem werden immer symmetrisch 2 Seiten gleichsetzt. Das Problem liegt darin, dass unsere Logik zum Lösen des Problems selber wieder zum Bestandteil der Logik beschrieben werden muss. Daher können wir scheinbar nur maximal 50% des Universums beschreiben? Der Rest muss aus nicht beschreibbarem Chaos bestehen. Das ist eine Definition von Chaos.

Die „nicht“-Weltformel

  1. Vereinfachungen müssen immer gemacht werden. (Was ist Wahrheit?)
  2. Die Vorstellung unendlich vieler Symmetrien ist real.
  3. Chaos ist real. (sogar mathematisch in der Wurzel aus 2)
  4. Auch Lügen sind real. Ebenso, dass wir uns selber belügen.
  5. Statistisch muss es auch Zeitpunkte geben, an denen die ganze Welt nur aus Lügen besteht.
  6. Lügen kann sowohl zu einer besseren, als auch zu einer schlechteren Welt führen.
  7. Gut und Böse sind nur 2 Seiten derselben Medaille (Quantelung)
  8. Somit nichts gut oder böse, aber vieles beschreibbar.
  9. Jeder ist daher verpflichtet für eine bessere Welt zu arbeiten.
  10. Aber wenn alles Gleichgewichtsprozesse sind, haben wir ja gar keine Chance.
  11. Eine Weltformel muss unverständlich bleiben, da ansonsten die Asymmetrie der menschlichen Existenz verloren gehen würde.

Kann jeder ein fraktales Universum verstehen?

Prinzipiell unlösbare Probleme

Die „Ja, aber“ - Theorie

  1. Im sehr Großen können Dinge mit Hilfe der Relativitätstheorie beschrieben werden.
  2. Im sehr Kleinen können Dinge mit Hilfe der Quantenphysik beschrieben werden.
  3. Wir können das komplette „sichtbare“ Universum mit Hilfe von Symmetrien beschreiben.
  4. Zwischen Groß und Klein gibt es Dinge, dessen Beschreibung unendlich kompliziert ist. Irrationale Zahlen haben unendlich viele Nachkommastellen.
  5. Aufgrund von 4 muss eine "Theory of everything" mindestens unendlich kompliziert sein.
  6. Unendlich komplizierte Dinge sind nicht berechenbar und werden als Chaos definiert.
  7. Ob es eine "Theory of everything" gibt hängt davon ab, ob es kleinere Dinge als Quarks oder größere Dinge als Universen gibt.
  8. Aufgrund von 7 können wir daher Chaos im Universum nicht ausschließen.
  9. Wir können daher nicht wissen was oder wie viel im Universum berechenbar ist.