Die Betrachtung von Symmetrien in einem fraktalen Universum 

(Version vom 23.11.2012) 

1 Einleitung 

Eine Antwort nach dem Ursprung unserer Welt oder des Universums kann zur Zeit am ehesten von der Physik mit all seinen Theorien und Formeln erbracht werden. So viele physikalische Phänomene können beispielsweise durch einfache lineare Gleichungen angenähert werden. Und viele weitere durch quadratische Gleichungen oder Wurzelfunktionen. Es scheint, dass unser Universum ein Universum der Symmetrien und Muster ist. Die andere Seite, die aber genauso zu unserer Welt dazugehört, ist die Seite der chaotischen Prozesse die nur indirekt beschrieben werden können. Diese beiden Komponenten gehören aber immer zusammen. Sei es in Galaxien, Atomen, Wetterphänomenen oder menschlichen Gesellschaftsstrukturen. Kann es sogar sein, dass solche fraktalen Strukturen auch für den menschlichen Verstand oder gar für den mathematischen Formalismus der Physik gelten? In dem folgenden Text soll erklärt werden welche Symmetrien und Ähnlichkeiten unsere beiden großen physikalischen Theorien, die Relativitätstheorie und auch die Quantenphysik verbindet. Wir Menschen haben die Relativitätstheorie für sehr große aber fast statische Strukturen und die Quantenphysik für extrem kleine aber nahezu unendlich schnelle Prozesse entwickelt. Eine Vereinheitlichung dieser "letzten" beiden Theorien würde alle Details unserer extrem komplexen Welt erklären, was die Vereinheitlichung vermutlich unendlich kompliziert macht selbst wenn alle Vereinfachungen ausgenutzt werden könnten. Im nachfolgenden Text soll möglichst verständlich dargelegt werden, wie man unsere fraktale und komplizierte Welt doch zumindest annähernd begreifen kann. Dabei kann leider niemals alles bewiesen werden, sondern immer nur eine bestimmten Sichtweise dargestellt werden. 

2. Hauptteil 

2.1 Überlagerung von stehenden Wellen in bewegten Inertialsystemen 

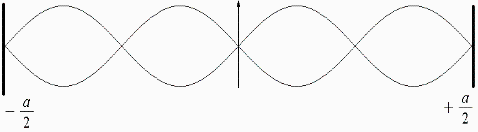
Beginnen wir mit Bekannten. Zunächst soll ein klassischer 3-dimensionaler euklidischer Raum betrachtet werden. In diesem System S1 soll eine Welle zwischen 2 Reflektoren mit dem Abstand a hin und her pendeln. Die Wellenlänge soll dabei genau so gewählt sein, dass sich eine stehende Welle ausbilden kann (siehe z.B. Mayer-Kuckuk, Atomphysik, Seite 54, Fig 24). 

Fig. 1   

Stellen wir uns nun vor, dass wir uns nun mit den Spiegeln in einem bewegten Bezugssystem S2 mit einer konstanten Geschwindigkeit v nach rechts bewegen. Die Welle soll sich dabei weiterhin in dem Medium von Bezugssystem S1 mit einer konstanten Ausbreitungsgeschwindigkeit c fortpflanzen.

Fig. 2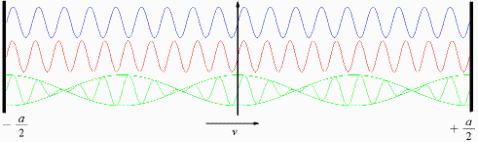   

Die obere Welle in Fig. 2 stellt die nach links laufende Welle und die mittlere die nach rechts laufende Welle dar. Wenn wir uns im Bezugssystem S2 befinden wird deutlich, dass die Ausbreitungsgeschwindigkeit der rechtsfließenden Welle nun c-v und für die linksfließende Welle c+v sein muss. Eine stehende Welle kann nun nicht mehr garantiert werden. Durch die Spiegelung der Welle an den nun bewegten Reflektoren ändert sich außerdem die Frequenz der Welle. Trotzdem ist in der resultierenden unteren Welle zu erkennen, dass sich bei bestimmten "gequantelten" Geschwindigkeiten immer noch stehende Wellen oder stehende Wellengruppen ausbilden können. Ermitteln wir nun einige Bezüge: 

[Gl. 1]    Zeitdauer für eine Wellenfront im Bezugssystem S1 für Strecke a 

[Gl. 2]    Zeitdauer für eine Rechtslaufende Wellenfront im Bezugssystem S2 für Strecke a 

[Gl. 3]    Zeitdauer für eine Linkslaufende Wellenfront im Bezugssystem S2 für Strecke a 

Wir ermitteln die Zeitdauern für einen kompletten Hin- und Rückweg im Bezugssystem S1 und S2. 

[Gl. 4]    Zeitdauer für eine Wellenfront für einen Hin- und Rückweg, in S1 

[Gl. 5]    Zeitdauer für einen Hin- und Rückweg in S2 

Setzen wir die Zeiten für einen kompletten Hin- und Rückweg gleich (konstante Zeit). Mit erhalten wir so einen Längenverzerrungs-Faktor / : 

[Gl. 6]   

[Gl. 6]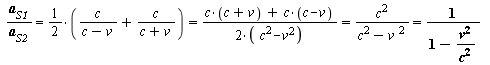   

Genauso können wir aber auch die Strecken gleich setzen (konstante Länge) und wir erhalten so einen Zeitverzerrungsfaktor / : 

[Gl. 7]      und    

[Gl. 7]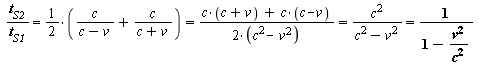   

Theoretisch kann der Grenzfälle einer konstanten Zeit genauso wie der Grenzfall einer konstanten Länge Sinn machen. In der Natur sind Extremfälle allerdings eher selten. Daher können wir davon ausgehen, dass sich ein Zwischenzustand einstellt. Betrachten wir dazu noch zwei andere Grenzfälle: 

- Ist die Anzahl der Wellenberge zwischen den Reflektoren sehr hoch, dann kann sich für sehr viele verschiedene Geschwindigkeiten eine stehende Welle ausbilden. Im Extremfall für unendlich viele Wellenberge muss dies für jede beliebige Geschwindigkeit möglich sein (siehe dazu auch im Abschnitt 3.2).  

- Ist dagegen nur ein einziger Wellenberg vorhanden, dann kann sich nur für v=0 eine stehenden Welle ausbilden.
 

2.2 Definition einer Zeit im 3-dimensionalen Raum 

Stellen wir uns nun noch eine etwas andere Sichtweise vor. Eine Wellenfront einer Kugelwelle soll sich in einem euklidischen Raum in einem Bezugssystem S1 ausbreiten. Die Ausbreitungsgeschwindigkeit ist in den 3 Raumdimensionen konstant c. Als Veranschaulichung dazu soll in dem Graph in Fig. 3 ein Surfer dargestellt sein, der sich mit einer konstanten Geschwindigkeit in Richtung Y-Achse in der Zeit bewegt. Die X-Achse soll eine Raumdimension darstellen. 

Fig. 3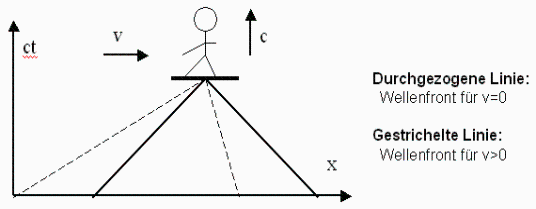   

Die Wellenfront der "Bugwelle" breitet sich also in positiver wie auch negativer Richtung der X-Achse mit c aus. Gleichzeitig dazu bewegt sich der Surfer in Richtung Y-Achse in der Zeit. Wir erhalten einen Ausbreitungskegel wie in Fig. 3 durch die durchgezogene Linie dargestellt. Ist die Fortbewegungsgeschwindigkeit des Surfers in der Zeit genau gleich der Wellengeschwindigkeit, dann bildet sich zwischen den Wellenfronten ein Winkel von exakt 90°. Nun soll sich der Surfer zusätzlich zur Bewegung in der Zeit auch noch in Richtung der X-Achse bewegen. Die Wellenfront soll in Fig. 3 durch die gestrichelte Line dargestellt werden. Um weiterhin einen 90° Winkel zwischen den "Bugwellen" zu erhalten, muss die Geschwindigkeit in der Zeit immer noch gleich der Wellengeschwindigkeit sein, aber nun nicht mehr Richtung Y-Achse, sondern schräg nach oben im 45°-Winkel bezüglich der Wellenfronten. Wir bezeichnen so etwas als Rotation. 

Für einen absoluten Zeitbezug ist nun aber eine konstante Geschwindigkeit Richtung Y-Achse erforderlich. Um einen 90° Winkel zwischen den Wellenfronten zu erhalten, kann dazu die Y-Achse über einen Faktor skaliert werden (Längenkontraktion). Wir ermitteln dazu die Zeitdauern, in denen die Wellenfront in dem nicht bewegten bzw. dem bewegten Bezugssystem eine Strecke a durchschreitet und erhalten die obigen Gleichungen Gl. 1-3 die wir schon bei unserer stehenden Welle erhalten haben. 

[siehe Gl. 1]    für eine Wellenfront im nicht bewegten System S1 (v = 0)  

[siehe Gl. 2]    für eine Rechtslaufende Wellenfront im bewegten System S2 (v > 0)  

[siehe Gl. 3]    für eine Linkslaufende Wellenfront im bewegten System S2 (v > 0) 

In unsere reale Welt, in der die Konstanz der Lichtgeschwindigkeit in allen Bezugssystemen gilt, legt die Ankunft einer Lichtwelle fest, wann ein Ereignisses eintrifft. Auf der rechten Seite erreicht die Welle im bewegten Bezugssystem S2 später ihr Ziel, als in S1 und deshalb muss unsere Uhr dort bezüglich S1 etwas vorgehen. Auf der linken Seite ist es umgekehrt. Unsere Uhr geht nach. Durch diese Definition einer zeitlichen Verzerrung können wir unsere Welt einfach so verbiegen, dass wir zu dem von uns gewünschten Ergebnis kommen, dass eine Welle eine Strecke a in jedem Bezugssystem in einer identischen Zeit durchläuft. In unserer Vorstellung "fließt" nicht nur die Welle, sondern auch die Zeit von einem Punkt aus in den umliegenden Raum. 

Stellen wir uns nun vor, dass sich unser Surfer in die entgegengesetzte Richtung -v bewegen soll. Die Grafik wäre genau um die Y-Achse gespiegelt. Bei dem Michelson-Morley-Experiment passiert aber genau das zu jedem Zeitpunkt, da sich ja die Lichtstrahlen immer in entgegengesetzte Richtungen bewegen. Oder anders ausgedrückt existiert so etwas wie eine "Vorwärtswelle" die sich vom Beobachter aus wegbewegt und eine "Rückwärtswelle", die sich wieder auf den Beobachter zubewegt. Wie können wir aber diese beiden Bilder überlagern? Die Lösung kann vielleicht so etwas wie eine Zickzack-Bewegung sein. Zu jedem Zeitpunkt soll sich der Surfer ein sehr kleines Stück nach links und anschließend ein ebenso kleines Stück nach rechts bewegen. Durch dieses Zerhacken der Wellen können die Verzerrungsfaktoren (für Raum und Zeit) erhalten bleiben und die Bewegung kann aus der Ferne aus betrachtet trotzdem gleichmäßig aussehen. Wir wollen es im Moment einfach bei diesem Bild belassen. 

2.3 Raum-Raum-Schleifen und Raum-Zeit-Schleifen 

Betrachten wir nun noch die Ausbreitungsfunktion einer Welle im Raum über einen Radius r. Die Gl. 8 soll dazu den Bezug zwischen den Raumdimensionen x,y,z und der Zeit skizzieren.  

[Gl. 8]      bzw.     

(Albert Einstein, Über die spezielle und die allgemeine Relativitätstheorie, Seite 94, Gleichung 10) 

Grundlage für eine Dimension ist dabei immer, dass sie linear unabhängig zu den anderen Dimensionen existiert. Dies gilt leider nur für die 3 Raumdimensionen und nicht für eine 4-Dimensionale Raumzeit. Wir können allerdings behaupten, dass die Z-Dimension das Ergebnis einer neuen "3-dimensionalen" X-Y-Zeit-Welt sein soll. Wir erhalten eine Welt, in der die Zeit als linear unabhängige Dimension existiert. 

[Gl. 9]     bzw.     

Wenn wir die Aufteilung etwas anders vornehmen, so bekommen wir so etwas wie eine Funktion für einen Kreis. Eine X-Y-Schleife ist dann gleich einer Z-Zeit-Schleife oder umgekehrt eine Z-Zeit-Schleife ist gleich einer X-Y-Schleife: 

[Gl. 10]   

[Gl. 11]   

Es gibt 6 prinzipiell mögliche Zusammensetzungen: 

 X-Zeit-Schleife    Y-Zeit-Schleife     Z-Zeit-Schleife 

 X-Y-Schleife       X-Z-Schleife        Y-Z-Schleife 

Mit Hilfe der Eulerformel kann ein rotierendes System sehr schön als komplexe Exponentialfunktion in einer Formel abgebildet werden. Die Wellenfunktion ist eine Funktion des Raumes und der Zeit. Hier soll x explizit kein Raumvektor, sondern nur eine X-Dimension wiederspiegeln. Konstanten sind außerdem noch die Amplitude A, die Wellenzahl k und die Kreisfrequenz ω. Bei einer Aufteilung auf Raum und Zeit stellen wir fest, dass bei genau der Hälfte aller möglichen Schleifen ein Raum aufgespannt wird. Dabei ist die Aufteilung zwischen Raum und Zeit eigentlich willkürlich (Bezug 4D-Raumzeit). 

(Mayer-Kuckuk, Atomphysik, Seite 225, A 1.22) 

2.4 Lineare Beziehungen zwischen Bezugssystemen 

Betrachten wir noch einmal 2 Bezugssysteme S1 und S2 in einem euklidischen Raum. In dem Bezugssystem S2 sollen einmal alle Längen bezüglich des Bezugssystems S1 um den Faktor gestaucht werden. Umgekehrt müssen sich dadurch im Bezugssystem S1 bezüglich des Bezugssystems S2 alle Längen um genau den gleichen Faktor strecken oder anders ausgedrückt, um einen umgekehrten Faktor stauchen. Beide Faktoren miteinander multipliziert ergeben immer 1. Dies gilt für alle linearen Systeme wie den 3 Raumdimensionen und auch für die Zeit. 

[Gl. 12]   

[Gl. 13]   

2.5 Konstanz der Lichtgeschwindigkeit 

Fügen wir nun die fundamentale physikalische Bedingung der konstanten Lichtgeschwindigkeit in allen Bezugssystemen ein. Auch in einem euklidischen Raum gilt, dass die Wellengeschwindigkeit konstant bleibt, wenn wir in einem Bezugssystem S2 die Zeit um einen Faktor f langsamer laufen lassen und gleichzeitig dazu den 3-Dimensionalen Raum um den gleichen Faktor f stauchen. Dies ergibt sich direkt aus der Tatsache, dass eine von einer Welle durchschrittenen Strecke a dividiert durch die benötigte Zeitdauer t eine konstante Wellengeschwindigkeit c ergibt. 

[Gl. 14]    

Wir können also lineare Systeme beliebig skalieren. Außerdem muss es möglich sein, dass wir ein beliebiges System in der Länge mit einem Faktor und in der Zeit mit einem Faktor so skalieren, dass wir eine auf 1 normierte Wellengeschwindigkeit erhalten. Wir folgern, dass c nur als Transformationsfaktor zwischen den physikalischen Größen Raum und Zeit zu sehen ist. Ansonsten ist alles was existiert relativ, skalierbar und symmetrisch. 

[Gl. 15]    

2.6 Die Überlagerungsbedingung 

Wie in der Quantentheorie vorgeschlagen, wollen wir jetzt unsere Reflektoren der stehenden Welle aus Abschnitt 2.1 durch eine 2te stehende Welle ersetzen. Eine stehende Welle soll sich also an sich selbst spiegeln und außerdem mit sich selbst überlagern (Mayer-Kuckuk, Atomphysik, Seite 52, Fig. 23 und Seite 70, Fig. 29). Mehr noch, die Welle soll sein eigenes Ausbreitungsmedium sein. Stellen wir uns also vor, dass wir uns in einem neuen Bezugssystem S0 befinden. Bezüglich dieses Systems soll sich das System S1 aus Abschnitt 2.1 mit der gleichen Geschwindigkeit v* nach links bewegen, wie sich das System S2 mit v* nach rechts bewegt. Durch die entgegengesetzten Geschwindigkeiten sollen die Systeme S1 und S2 im System S0 spiegelsymmetrisch zueinander sein. 

Fig. 4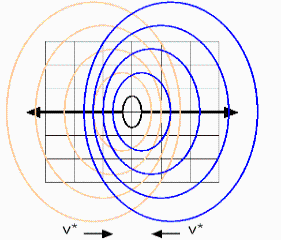   

Versuchen wir im System S0 noch einmal die Systeme aus dem Abschnitt 2.1 zu überlagern. Zumindest in einem sehr kleinen Punkt im Ursprung der Welle muss dies prinzipiell möglich sein. Um Bezugssysteme vergleichen zu können, fordern wir für beide Systeme, dass diese die exakt gleichen zeitlichen, wie auch räumlichen Verzerrungsfaktoren aufweisen. Wir fordern nach Gl. 12 dass für Raum und Zeit gilt. Nach Gl. 13 muss aber auch gelten. Es folgt direkt . Dies steht aber im direkten Konflikt mit Gl. 6 und 7 die zwangsweise fordern. 

Um alle Kriterien gleichzeitig zu erfüllen, müssen wir schon annehmen, dass ein Faktor / und sein Umkehrfaktor / nur existiert, wenn wir eine zusätzliche (Raum-)Dimension zulassen. Ähnliches gilt für die Zeitverzerrungsfaktoren / und / . Die Zusatz-Dimension kann aber auch wieder die jeweils andere Dimension sein. Wir benötigen also nur eine weitere Dimension. Bezogen auf Fig. 4 stellen wir uns vor, dass sich die Fläche in den Bildschirm rein- bzw. rausdreht. Für uns sichtbar wird dabei aber immer nur die Verzerrung. Für eine mathematische Betrachtung sehen wir uns noch einmal die Wellenfunktion aus Abschnitt 2.3 an, die wir hier noch zwei mal um einen Phasenwinkel ϕ drehen wollen: 

[Gl. 16]   

In Gl. 16 wurden die Phasenwinkel aus dem Exponenten rausgezogen und als Produkt geschrieben. Wir wollen die nun als Verzerrungsfaktoren auffassen und erwarten daher, dass die neuen Verzerrungsfaktoren a/a' und t'/t bezüglich S0 und S1 bzw. S0 und S2 genauso miteinander multipliziert werden können, wie die . Beide Rotationen zusammen sollen anschließend die Verzerrungsfaktoren zwischen S1 und S2 ergeben. Stellen wir noch sicher, dass die Skalierungsfaktoren auch vergleichbar sind. Von unserem Beobachtersystem wird daher in dem Fall 1 nur in eine Richtung rotiert und im Fall 2 aber zu beiden Seiten. Bezüglich des Beobachters sind die Rotationen und auch die Skalierungen gleich und mögliche rekursive Abhängigkeiten werden so ausgeschossen. 

Fall 1: Beobachtersystem ist S2. Verzerrungsfaktoren sind / und / bezüglich System S1. 

       = Beobachtersystem ist S1. Verzerrungsfaktoren sind / und / bezüglich System S2. 

Fall 2: Beobachtersystem ist S0. Verzerrungsfaktoren sind a/a' und t'/t bezüglich S1 und bezüglich S2. 

         Die Faktoren bezüglich S1 und S2 sollen aufgrund der gleichen Geschwindigkeit v* gleich sein. 

         Die Drehrichtungen von S1 und S2 bezüglich S0 sollten gegenläufig sein. 

Es folgt: 

[Gl. 17]   und    

Setzen wir Gl. 6 und 7 in Gl. 17 ein: 

[Gl. 18]    (Gl. 6 und 7) 

Bezüglich der Kehrwerte ergibt sich einmal ein Stauchungsfaktor und einmal ein Streckungsfaktor. Beide Faktoren machen Sinn. Trotzdem ist uns eine Variante geläufiger: 

[Gl. 19] 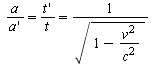    (der Lorentz-Faktor)  

(Wolfgang Pauli, Encyklopädie der Mathematischen Wissenschaften Bd. V, Seite 544)  

Die Faktoren für Raum- und Zeitverzerrung sind gleich. Bei einem Gleichgewicht zwischen Raum und Zeit war dies auch genau das, was wir aufgrund der Forderungen erwartet haben. 

2.7 Größenskalierungen 

Der Gleichgewichtsprozess aus dem vorherigen Abschnitt 2.6, soll hier noch einmal eine logische Begründung erhalten. In Fig. 4 ist deutlich zu erkennen, dass eine Links-Bewegung nicht direkt mit einer Rechts-Bewegung überlagert werden kann, da sich beide Wellen spiegelbildlich zueinander verhalten und immer weiter auseinander laufen. Der einzige Bereich, der einigermaßen identisch ist, ist der Bereich direkt um den Ursprung der Welle. Die Berechnungen gelten also nur für eine Welle mit einer unendlich kurzen Reichweite. Dies steht aber im Konflikt mit der Vorstellung, dass sich in Fig. 2 nur für bestimmte "gequantelte" Geschwindigkeiten eine stehende Welle ausbilden kann. Um für alle Geschwindigkeiten stehende Wellen ausbilden zu können, benötigen wir unendlich viele Wellenberge. Dies wiederspricht aber wieder dem Bild der unendlich kleinen Kugelwelle. So wie es aussieht, gilt die Lorentz-Transformation daher nur im Grenzfall, wenn sich sehr kleine Wellenstrukturen mit sehr großen Wellenstrukturen überlagern. 

In der Relativitätstheorie kann mit dem Relativitätsprinzip auf ein absolutes Bezugssystem wie den Äther verzichtet werden. Dies wird mit dem beschriebenen Prinzip insoweit bestätigt, dass das Ausbreitungsmedium einer Welle wieder die Welle selber ist. Zusätzlich dazu soll mit dem Prinzip aber auch auf eine absolute Größe verzichtet werden können. Wichtig ist nur der Bezug zwischen Länge und Zeit und auch der kann prinzipiell skaliert werden. Wenn wir uns einige bekannte Strukturen ansehen, Quarks - Protonen - Atome - Planeten - Sterne - Galaxien - Galaxienhaufen - Universen - macht es nicht unbedingt Sinn, das Quark zwangsweise als das Kleinste und das Universum als das Größte anzusehen. In der Physik wird es vermutlich eher darauf hinauslaufen, dass wir aufgrund von messtechnischen Beschränkungen einfach nicht mehr erkennen können, ob es noch etwas Kleineres oder etwas Größeres gibt oder nicht. Ähnlich wie beim dem Welle-Teilchen-Dualismus kann auch hier durch unterschiedliche Perspektiven der gleiche Sachverhalt unterschiedlich dargestellt werden. Vermutlich ist es daher sogar prinzipiell unentscheidbar, ob sich unser Universum ausdehnt oder nicht, da die Rotverschiebung weit entfernter Objekte sicherlich auch als Eigenschaft des "gekrümmten" Raumes am Rand einer Blase in einem Multiversum aufgefasst werden kann. 

2.8 Definition von Energie und Energiedichte 

Betrachten wir die Skizzen einer stehenden Welle in Fig. 5. In den 3 Abbildungen ist eine Linie vom rechten Reflektor zum linken Reflektor immer gleich lang, egal welche Frequenz zugrunde gelegt wird. Dies gilt nicht nur für eine Dreiecksform sondern immer, wenn die Welle komplett (Raumrichtung x und Amplitude A) um einen Faktor n gestaucht wird und anschließend n mal zwischen die Reflektoren eingefügt wird. Als Begründung kann das Skalarprodukt angegeben werden, bei dem durch die Skalierung aller Komponenten eines Vektors mit einem Faktor n, auch der Vektor selber mit diesem Faktor n skaliert wird. 

Fig. 5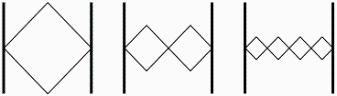   

Die Skalierungsbedingung gilt auch ganz speziell für alle Sinuswellen, bei denen die Steigungen in den Nulldurchgängen betragsmäßig immer 1 sind: 

[Gl. 20]      Nulldurchgang z.B.bei x=0     

In Fig. 5 muss die im System enthaltene Energie in allen Fällen gleich sein, da Gummibänder aufgrund gleicher Linienlänge immer gleich stark gespannt wären (siehe auch Abschnitt 3.3). Allerdings ist die Energiedichte in dem gestauchten System bezüglich des nicht gestauchten Systems um einen Faktor n größer, da die Amplitude um genau diesen Faktor n kleiner wird. In dem gleichen Raum kann also n-mal so viel Energie gespeichert werden. 

Vergleichen wir nun einen Skalierungsfaktor n für eine Längenverzerrung (nach Gl. 6) und bei selbst interferierenden Wellen den Lorenzfaktor (nach Gl. 19). Da der Lorenzfaktor nach Abschnitt 2.6 auch als Rotation in einem höherdimensionalen Raum aufgefasst werden kann, soll für die Geschwindigkeit nur ein ganz besonderer Wert von 1/ vorgegeben werden. Dies entspricht einer Rotation von π/4 bzw. 45° und ist in der 3D-Welt eine wichtige Symmetrie. 

[Gl. 21]    

Setzen wir nun für in die Gleichungen 6 und 19 ein, so erhalten wir: 

[mit Gl. 6]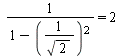   

[mit Gl. 19]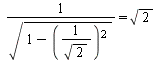   

Ausgehend von einem euklidischen Raum wird eine quadratische Funktion zu einer linearen Funktion, wenn eine Welle mit sich selber interferiert. Wenn im euklidischen Raum also um die X-Achse und die Y-Achse rotieren werden muss, so muss bei selbstinterferierenden Wellen nur noch um eine Achse rotiert bzw. skaliert werden. Die andere Rotation findet in der Raumzeit statt. Ausgehend von einem euklidischen Raum wird die Energie, die in einem schwingenden System enthalten ist (siehe Abschnitt 3.3), bei selbstinterferierenden Wellen zu bzw. zu je nachdem, ob die Länge (Rotation um Y-Achse) oder die oder die Amplitude (Rotation um X-Achse) skaliert wird. Fordern wir eine konstante Amplitude , dann ergibt sich ein Bezug zum Plankschen Wirkungsquantum: 

[Gl. 22]      Bezug zum Plankschen Wirkungsquantum 

In Fig. 5 wurden Sinusschwingungen durch einfachere Quadrate dargestellt. Erst durch diese Vereinfachung können wir, wie in Fig. 6 dargestellt, fraktale Muster auf eine für uns verständliche Weise darstellen. 

Fig. 6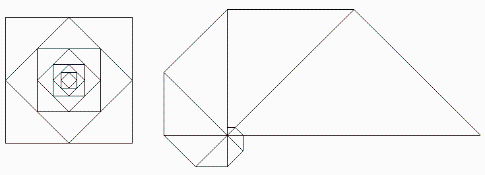   

2.9 Gekrümmte Bahnen 

In unserer Vorstellung soll in einem euklidischen Raum ein Objekt auf einer kreisrunden Bahn gehalten werden. Rotiert ein Objekt um ein Zentrum mit konstanter Geschwindigkeit v, dann ist die Strecke, die für eine Rotation des Objekts um einen Winkel α zur Verfügung steht, proportional abhängig zum Radius r. Dies leitet sich direkt aus dem linearen Zusammenhang zwischen Umfang U und Radius r in einem Kreis ab (). Wir müssen also für einen kleineren Radius r bei gleicher Geschwindigkeit antiproportional mehr Kraft aufwenden, um ein Objekt auf der Kreisbahn zu "halten". Dies soll nun durch einen entsprechenden Energiedichtegradienten hervorgerufen werden. 

[Gl. 23]   

Fig. 7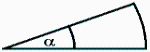   

Das Ganze sollte grundsätzlich auch für Wellen mit konstanter Geschwindigkeit v=c gelten. Um die Welle auf seiner Bahn zu halten, stellen wir uns vor, dass die Welle so wie in einer Linse "gebrochen" wird und so auf seiner Bahn gehalten wird. Die Energiedichte muss im Potential ähnlich wie im ersten Fall mit kleineren Abständen r zum Zentrum hin antiproportional größer werden. Alle Wellen, die in so einer Schleife "gefangen" sind, bezeichnen wir als Masse. Hat Masse in einer Scheibe wiederum eine 1/r-Verteilung, dann rotieren alle Objekte mit der gleichen Winkelgeschwindigkeit.

Relativistische Betrachtung des Großen:  

Eine stehende Welle (aus Abschnitt 2.1) kann auch für bewegte Systeme existieren, wenn der Raum oder die Zeit dazu verzerrt wird. Im Grenzfall für eine maximale Geschwindigkeit v=c muss der Betrachtete Raum nach Gl. 6 bzw. 7 unendlich stark gekrümmt sein (Unendlichkeitsstelle in Fig. 8 an der Y-Achse). 

Quantenmechanische Betrachtung des kleinen: 

Auf der anderen Seite muss der Raum unendlich stark gestreckt werden, wenn eine Lichtwelle im Randbereich des Potentialtopfs durch die Betrachtung mit v=0 zum Stillstand kommt. Dies ist der Zeitpunkt, wenn ein schwingender Punkt die Bewegungsrichtung ändert. Für einen Beobachter muss immer noch v=c gelten (Unendlichkeitsstelle in Fig. 8 an der X-Achse).  

Modellvorstellungen eines Gleichgewichtsprozesses: 

- Relativistisch rotiert nur ein Objekt nur verlustarm um eine Masse, wenn dieses unendlich schwer ist. Ansonsten werden immer Teilchen in Form von Gravitationswellen abgegeben. Ein Gleichgewicht stellt sich erst für ein 1/r Potential ein (Masseverteilung in maximal chaotischen Galaxien). 

- Quantenmechanisch möchten Bosonen gerne den gleichen Zustand einnehmen. Dies führt dazu, dass eine Struktur nicht auseinander fließt. Und die Eigenschaft von Fermionen führt dazu, dass alle quantenmechanischen Zustände belegt werden und die Welle dadurch nicht ins Zentrum fällt. Auch hier bildet sich ein Gleichgewicht. 

Fig. 8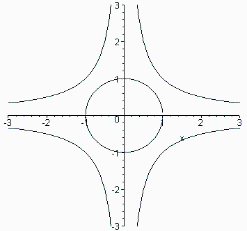   

So wie es aussieht, gilt die Relativitätstheorie als Grenzfall im Großen und die Quantentheorie als Grenzfall im Kleinen. Energie überlagert sich in seiner kompaktesten Form immer zu so etwas wie diesem Coulomb-Potential. Für größere Gradienten bricht die Welle und fließt auseinander. Ein Bereich mit kleinerer Steigung wird sofort mit neuen Teilchen gefüllt. Im Grenzfall, für eine unendlich große Frequenz der Welle, ergibt sich für das Potential auch der Grenzfall einer unendlich großen Energie. Ein reales Energiepotential unterscheidet sich davon, dass die Energie durch ständige Interaktionen der inneren Teilchen nie einen unendlich großen Wert annehmen kann. Erst in einem "nicht idealen" Coulomb-Potential kann es möglich sein, dass sich im Potentialfeld wieder neue Strukturen bilden. Z.B. ein Elektron im Potentialtopf eines Protons. 

Am Rand ist das Coulomb-Potential durch die "stehenden Wellen" immer etwas zackig. Wenn sich etwas bewegt, dann immer um eine ganze Wellenlänge. So eine stockende Bewegung neigt natürlich wieder zu Schwingungen, was Teilchen in der Umgebung anregt. Vermutlich haben sogar alle Teilchen in unserem Universum gemeinsame Resonanzfrequenzen. Die Theorie eines Führungsfeldes soll beispielsweise den Welle-Teilchen-Dualismus bzw. die Bellschen Ungleichungen erklären. Können wir uns unsere Welt von Quark bis zum Universum also als unendlich komplex und verknoteten Raum vorstellen? Ist die Vorstellung eines Fraktals von Spiralen die einfachste Sichtweise unseres Universums? So wie es aussieht hat unser Universum aber noch weitere Symmetrien, wie die einer Kugeloberfläche. Wichtig ist, dass rein gar nichts absolut ist. Auch die Gravitationskonstante und die Lichtgeschwindigkeit dürfen nur abhängig vom Ort aus existieren, von dem aus sie betrachtet werden. Die Gravitationskonstante kann vielleicht als "Rest"-Energie bezeichnet werden, die nach allen Teilcheninteraktionen in unserem Sonnensystem noch übrig bleibt. Das Gegenstück dazu ist die Lichtgeschwindigkeit. In einem unendlich dichten Medium läuft nach Einstein die Zeit unendlich langsam ab, bzw. ist die Lichtgeschwindigkeit unendlich langsam. Am Rand unseres Universums muss die Lichtgeschwindigkeit daher unendlich groß werden. Oder anders ausgedrückt muss bei konstanter Lichtgeschwindigkeit der Raum unendlich groß werden. Raum und Zeit erzeugen sich quasi gegenseitig und bilden unser Universum. Es ist also alles relativ, invertierbar und fraktal, aber was passiert, wenn die Menschen akzeptieren könnten, dass sie selber ein Teil dieses Systems sind? 

Fig. 9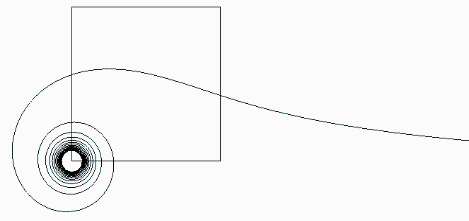   

3 Mathematischer Anhang 

3.1 Herleitung einer stehenden Welle 

Es kann gezeigt werden, dass sich 2 entgegengesetzt fließende Wellen zu einer stehenden Welle überlagern können (Mayer-Kuckuk, Atomphysik, Seite 35, Gleichung 2.9). 

[Gl. 30]  


 

Bei der neu entstandenen überlagerten Welle ist der zeitliche Faktor nicht von x abhängig. Die Phasenlagen bleibt also über die Zeit konstant. 

3.2 Herleitung zur Überlagerung von sehr hochfrequenten Wellen in bewegten Systemen 

Zwei gegenläufig laufende Wellen sollen zu einer stehenden Welle überlagert werden. Dabei soll eine Welle um einen Phasenwinkel ϕ verschoben sein. Wenn sich in einem bewegten Potentialtopf stehenden Wellen ausbilden sollen, muss diese Bedingung gegeben sein. Die stehenden Welle soll dabei genau die gleiche Form, sowie die gleiche Frequenz und Wellenlänge aufweisen, wie die Ursprungswellen. 

[Gl. 31]  

 

Es muss dazu gelten, dass die Phasenverschiebungen genau einem vielfachen der Wellenlängen entspricht. Dann kann die Phasenverschiebung ignoriert werden. Für sehr große Frequenzen ω wird dabei auch n sehr groß. Der Schritt zur nächsten natürlichen Zahl n+1 wird im Verhältnis dazu sehr klein. Die Wahrscheinlichkeit, dass sich für ein auch eine stehenden Welle ausbilden kann, steigt für eine höhere Frequenzen immer weiter an. Und zwar bei großen Frequenzen proportional zur Frequenz. 

3.3 Herleitung ungedämpfte harmonische Schwingungen 

Betrachten wir eine ungedämpfte harmonische Schwingung. Die Gesamtenergie ergibt sich dabei aus der potentiellen Energie und der kinetischen Energie . (Kuchling, Taschenbuch der Physik, Seite 187 und 196). 

[Gl. 32]   

 k = Richtgröße
 m = Masse
 v = Geschwindigkeit
 y = Auslenkung 

Durchläuft die Welle gerade den Nullpunkt, so ist und . Außerdem ist die Geschwindigkeit im Nulldurchgang maximal . Mit folgt: 

[Gl. 33]      oder     

Die Energie ist quadratisch proportional zur Amplitude und zur Kreisfrequenz. Amplitude und Frequenz sind bei konstanter Energie und Masse antiproportional zueinander. 

4. Offene Fragen 

- Wieso hat auch in einem großen Atomkern jedes Proton sein eigenes Elektron? Woher kommen solche Schwingungsmuster? Hat das Elektron einen Spin, der aufgrund der Struktur der Quarks zustande kommt? 

- Wie viele Symmetrien haben Elementarteilchen? Worin unterscheiden sich Teilchen von Antiteilchen? Fermionen von Bosonen? Rechtshändige von linkshändigen Teilchen (z.B. Neutrinos)? Wieso zerfällt beispielsweise ein Neutron in ein Proton, ein Elektron und ein Antineutrino? Aufgrund der Definition? 

- Kann ein schwarzes Loch als Elementarteilchen aufgefasst werden? Kann man unser Universum auch als "Elementar"-Teilchen auffassen? Dies könnte die Rotverschiebung sehr weit entfernter Objekte erklären, ohne dass sich das Universum dabei ausdehnen muss. Ist dies auch eine Erklärung für dunkle Materie? 

- Genau die Hälfte der Schleifen-Möglichkeiten aus Abschnitt 2.3 spannen einen Raum auf. Ist die im Universum enthaltene Energie daher je zur Hälfte auf Zeit und Raum aufgeteilt? Teilt der erste Symmetriebruch unseres Universums also in Raum und Zeit? Kann eine Symmetrie mit Information gleichgesetzt werden? 

- Wieso sind alle Protonen so ähnlich und haben alle die gleiche Masse? Wird im extrem Kleinen wie auch im extrem Großen alles ähnlicher symmetrischer, weil man bestimmte Symmetrien besser erkennt? Über Zustände, die sehr schnell ablaufen, kann auch in einem sehr kleinen Raum ausreichend Information gesammelt werden, um Symmetrien lokalisieren zu können. Sind die Prozesse dagegen langsam, fast statisch, dann muss auf der anderen Seite ein ziemlich großer Raum betrachtet werden, um Muster aufspüren zu können. Ist dies in Formeln abgebildet die Quantenphysik und die Relativitätstheorie? 

5. Literatur 

Dr. rer.nat. Theo Mayer-Kuckuk: Atomphysik Eine Einführung 2. Auflage 1980 

Dr. rer.nat. Theo Mayer-Kuckuk: Kernphysik Eine Einführung. 6. Auflage 1994 

Albert Einstein: Über die spezielle und die allgemeine Relativitätstheorie. 21. Auflage 1969 

Wolfgang Pauli: Relativitätstheorie. 2000 (Originalausgabe 1921 erschienen in der Encyklopädie der Mathematischen Wissenschaften Bd. V) 

Joseph Polchinski: WHAT IS STRING THEORY? 1994 

Frank Close: Das Nichts verstehen. Originalausgabe: The Void. 2007  

Kuchling: Taschenbuch der Physik. 15. Auflage 1995